Muhammad Sabieh Anwar
Physlab, Department of Physics, Syed Babar Ali School of Science and Engineering, Lahore University of Management Sciences (LUMS), Opposite Sector U, D.H.A. Lahore 54792, Pakistan
This is a record of two demonstrative lectures given by the author on the “Holistic Teaching of Science: A Teacher Training Workshop”, organized by the Pakistan Innovation Foundation and sponsored by the Templeton Foundation on 22 and 23 December 2019. The account of these lectures has been transcribed by Maleeha Waqar and edited by the author, Farah Nadeem, and Dr. Yasira Waqar. Experiments included in this description are built by the author and Azeem Iqbal, Hafiz Rizwan, Umar Hassan, Khadim Mehmood, and Waseem Ashraf from Physlab.
You can also download the PDF version here.
SABIEH: My name is Muhammad Sabieh Anwar, and  I wonder why Dr. Athar Osama always asks me to participate in these workshops on the nature of science. I am a practitioner of science, just an operational scientist, and in my daily life, care little about the nature or method of science. Generally, when we are doing science in laboratories, or on our writing desks, we are least concerned about the philosophy and the method of science—it is somehow inside us. We are trained as scientists and we usually don’t think about the philosophy, nature, and interpretation of science. We don’t ask questions such as, “Why are we doing this?”
I wonder why Dr. Athar Osama always asks me to participate in these workshops on the nature of science. I am a practitioner of science, just an operational scientist, and in my daily life, care little about the nature or method of science. Generally, when we are doing science in laboratories, or on our writing desks, we are least concerned about the philosophy and the method of science—it is somehow inside us. We are trained as scientists and we usually don’t think about the philosophy, nature, and interpretation of science. We don’t ask questions such as, “Why are we doing this?”
However, as scientists, when we go to bed every night and we think about how we spent our day in the laboratory, these interpretative ideas do sometimes come to our minds. Somehow, when we leave the learning environment as science graduates, we are already trained to work with a mindset called the
“nature of science” or the “method of science”
In fact, just before me, Prof. Nidhal gave a broad overview, a sketch, of the nature and methodology of science. There could be many variations and nuances to his description as there is no absolutely agreed method of science. There are areas of science that work rather differently from others. Moreover, there are raging debates that go on about what science really is.
What I am only going to do today is give you a feel of different kinds of experiments and how big a role, if they play one at all, in the methodology of science. I will give you some examples of fact, hypothesis, conjecture, theory and law. I will also give you examples from history. I will also talk a little bit about interpretation, but my main emphasis is on talking about experiments and how they are the linchpin of science.
I start off with a quotation attributed to Ibn al-Haytham. When the Muslim scientists were at the heyday of doing science, there existed a well-established tradition of the shukook literature. Shukook is the plural of shak, meaning criticism or critique. So, this is a critique of a famous scientist of another famous fellow scientist, Ptolemy. Read through this excerpt together with me.
“Truth is sought for its own sake; and as for anything sought for its own sake, one is simply concerned with finding it. But finding the truth is difficult and the road to it is steep, and truths are plunged in uncertainties. People are naturally inclined to think well of scientists, so that one who looks into the books of scientists (when he lets himself become slack with his natural inclination and make his goal [only] the understanding of what they have stated and the extent of what they put forth), the “truths” will be reached by him, which are the things that they have intended and the purposes that they have indicated. But God has not made scientists immune from deficiency and he did not protect their science from shortcoming and defect. If that were so, scientists would not differ on anything in the sciences and their opinions would not vary at all concerning the true nature of things; but the facts are otherwise. Thus, the seeker of the truth is not one who studies the writings of the ancients, and, following his natural disposition, puts his trust in them, but rather the seeker of truth is suspicious in his opinion of them, hesitant in what he understands of them, repeating the proofs and demonstrations and not the words of the sayer who is [after all only] a person, characterized by a variety of defects and deficiencies. It is necessary for one looking into the books of the sciences if his goal is to know truths, to make himself an adversary to all that he finds therein and turn his thought to their text and all their marginalia and to contest them from all sides and directions. And furthermore, he should be suspicious of his own self when he is being contentious so he treats them neither unjustly nor gently. Then if he follows this path the truths will become uncovered for him and what he found difficult in the deficient and obscure words of his predecessors will be clear1.”
One would like us to believe that the ultimate objective of science is to find the truth. However, scientific truths are different from religious truths. In science, truths are colored by uncertainties. This quotation is a beautiful rendition explaining the role of uncertainties which cannot be simply discounted as mistakes. Uncertainties are meaningful and are inherent in the process of science. Tomorrow, I will perform an experiment just to show you that.
Science, remember, is a human endeavor, an effort made by humans for humans. God may have ordained, ‘go and understand nature’ but after all scientific investigation and being curious about our natural surroundings and even making it into a formal enterprise, it is a human effort. It is done by humans and is therefore prone to errors. But uncertainties are deeper and are inextricably linked with the scientific method. Errors are mistakes and can be avoided but uncertainties are an integral component of the scientific endeavor. Uncertainty, noise, and complexity are the hallmarks of science.
In his statement, Ibn al-Haytham is talking about scientific opinions. The opinions of scientists are just like the opinions of other ordinary human beings and can be highly variegated. Even though a scientist forms his opinions in a mathematically rigorous, systematic, informed and scientifically enlightened fashion, scientific opinions will still differ from one scientist to another.
In religious knowledge, we espouse the concept of sanad which is based on a succession of transmissions of an opinion or tradition. The individual links of the chain are analyzed for their veracity. This analysis bestows certain transmitters with greater authority over others. The authority of the transmitters eventually vindicates the tradition. This chain of relegation is important in religious tradition, but that may not be the case in scientific matters wherein, in most cases, you do not take for granted anything that the ancients or predecessors say. Therefore, science is not tradition-oriented, it is contrarily, evidence-based.
A large portion of scientific development is based upon suspicion, questioning nature, and the validation of the results of experiments. It doesn’t mean that you become a perennial skeptic, and are always questioning and criticizing, but it means that you do have an open and tolerant mind because your opinions are subject to change, refinement, and improvement. This journey from hypothesis to scientific fact requires repeatability and reproducibility. It is through repeated observations that a hypothesis or conjecture is elevated to the status of a scientific fact. Consequently, the touchstone is not just what others have said, it’s what others have done, how they have presented the results, and if those same results are a posteriori, achieved a sufficient number of times in variable circumstances.
A scientist is supposed to be a self-introspective. When he performs an experiment and observes something, he always asks questions. This is a trait of a scientist and you will not find this trait probably in matters of religion. This is how the nature and epistemology of science is different from that of religion. I, by no means, am implying that one is superior to another, it’s that these bodies of knowledge work in different manners. They have differ- ent modus operandi and have different routes of building up knowledge. The statement from Ibn al-Haytham is the epitome of what the scientific method is and helps you read into the mind of a scientist.
Here is another quote that I really like. It’s from Francis Bitter, an experimental scientist, who worked in magnetism and wrote this little book titled ‘Mathematical Aspects of Physics’. What he is describing here is an image of an experimenting scientist. Let’s read through it.
“This chapter is intended to introduce the reader to the peculiar fascination of collecting and examining facts, the kind of facts that are called the data of science. At first glance the man who peers for long, long hours through a telescope at the stars, who gets stiff and cold and often discouraged trying to get a few bet- ter observations than actual circumstances at the moment per- mit, such a man will seem a “peculiar” sort of fellow. In general, the kinds of observation that a physicist makes, measuring little marks or the spot of light on a scale controller by an electric me- ter, or, nowadays, the pages and pages of numbers typed out for him by a machine, all these seem abstruse and forbidding to the casual eye. To tell the truth, there are times when this or any kind of work seems dull, exhausting, even fruitless. When, after days of trying, you still can’t find the leak in the vacuum sys- tem, or when, after you patiently have fitted an elaborate piece of apparatus together, an oscilloscope suddenly picks up a lot of meaningless “noise” from some unknown source, or when you have been working all days and all night on a series of measure- ments that must from some reason be completed at once, then of course the work is unattractive. The question to be answered does not concern the nature of such discouragement, but rather why any sane man would choose to be spending his time in the pursuit of experimental physics, even when everything is going just right, his apparatus performing as planned, and he can do his work seated in a comfortable chair2.”
One way to describe the nature of science is the way Prof. Nidhal has done which was an extremely systematic and methodological fashion but I can’t do that because I don’t understand the science that way. I am just an operational scientist who doesn’t understand the philosophy of the process but does know the process itself.
Remember, there is also some level of romance in doing experiments. Bitter’s statement gives a fair idea of the peculiar emotions and thought processes inside the mind of a scientist and he feels a unique affinity to the glamor of this process.
Whatever raw observation comes out of an experiment qualifies as data. I will give you examples of data later. The outcome of an experiment is data, sometimes heaps of data. Faisal showed you a text file which has the data of the genome of the E. coli bacterium. That data comes from DNA sequencing. You look at an oscilloscope or a meter, the needle vibrates to a certain position, you repeat the experiment and get a new position, that’s data too. That is the direct outcome of an experiment or an observation. The scientist then has to make sense of it.
How do we obtain data? First, we make an observation. An observer is the most basic kind of scientist, the most basic experimenter, on the lower end of the scientific food chain. What do I mean when I say pure observation? An observation works as follows. There is nature out there and you stand and stare at it, just look at it, you cannot interfere with it neither can you intervene in its processes. It is just there. You are only observing and noting down your observations, trying to generate data. Can you think of an observer scientist who has no role in his observation and cannot tinker with it?
PARTICIPANT: A child!
SABIEH: A child. Wow! Yes. Any more ideas? PARTICIPANT: An astronomer?
SABIEH: An astronomer! Yes! In the old times, the Babylonians, the Egyp- tians, or Hubble when they were observing the cosmos, they were pure observers. This person whom you all know, Umair Asim sitting at the back is mostly an observer. He looks at gamma bursts, planets and gaseous nebulae. He can’t go and change the course of a nebula. He cannot sit on a star and transmute its hydrogen to helium. Therefore, a traditional astronomer is an observer. However, what he receives from his telescope, and the network of telescopes, is just humongous amounts of data. That data becomes the foundation for more science, for conjectures and theories to formulate laws. Data is mostly the starting point.
Another famous example of an observer was Charles Darwin. He went to the Galapagos Islands and spent a lifetime there observing species of plants and animals. He was looking at the outcome of millions of years of evolution but he did not himself participate in the evolutionary process.

Darwin did not steer the evolutionary or natural selection process; he was merely observing. In older times, most sciences were of the observation kind. But a modern experimenter goes one step further. Remember science by its very nature, as Prof. Nidhal mentioned, is evidence-based and empirical. Something that cannot be verified by experiment or in a laboratory does not qualify as science. You can call it philosophy, but it is not science in the modern definition of the word.
Note that the definition of science has also evolved over the centuries, so this is from the vantage point of today. Coming back to the original question, how does an experimenter go a step further beyond the observer? Well, she starts to ask more serious questions about nature and starts probing, touching, massaging and controlling it. How does she do that? She does that with the help of instruments, tools and gadgets. She is no longer a bystander but actually participates in the cosmic drama. The experimenter is now becoming part of the natural process.
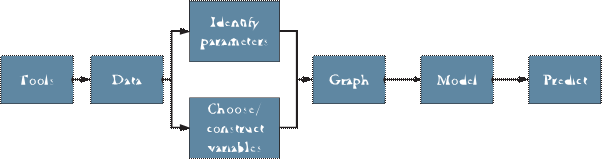
Let’s get to some more technical aspects. All kinds of experiments, if I were to sum it up, are composed of two classifications of data. One are the variables and the other are parameters. When you design an experiment and start doing science, even if it is theoretical science, you actually have at your disposal some controllable factors that you can change. You can change the pressure or perhaps the temperature of this room we are sitting in. That is a variable in your control. But you can’t change the volume of this room. You can’t change how big this room is, you have to be confined inside. If the walls of the room were however, made of stretchable balloon material, then it could be a different story, then the volume would also become a variable. So, what does an experimenter do? She first identifies all the variables and then asks a few questions to herself. What can I change with the money, equipment, gadgetry, time and tools that I possess? And what can I not change? Moreover, sometimes during the course of an experiment, she may become motivated to convert a parameter into a variable. This may help her get more insight and generate even newer data. So experiments revolve around identifying one’s variables and parameters.
But remember there are numerous other kind of scientists who are more traditional and classic and don’t classify data into variables and parameters. These are the explorers. For example, the anatomists who dissect a frog, observe and make drawings. Modern anatomy and physiology has developed through exploration. Geologists can also be explorers, finding what is inside the earth. An archaeologist is another kind of explorer who is unraveling artifacts and what lies under heaps of history.
I now like to demonstrate gravity to you. Through this example, I will illustrate what is a fact, an observation, and how does the scientific method generally work. We all know what gravity is. I throw this ball, it comes down. Is this an observation or a fact? Suppose you were just born, you have no access or knowledge of science and are just building up your experience. As a child you observe the ball to fall down. At this stage of your scientific development, you are making an observation, but as mature adults, we all know that this is always going to happen, even if you are not a scientist. So now the descent of the ball is being perceived as an established fact. Something that goes up, will come down. With experience, your opinion transitions from observation to fact. A repeated observation which becomes part of our collective experience is called a scientific fact.
An object falling down is an evidence-based scientific fact because this has happened millions and millions of times. From this we can start to develop conjectures: why does this ball even come down? Over the ages, scientists have come up with different explanations. Before gravity was discovered there were alternative explanations and hypotheses, but then all of them were chronologically filtered and as Ibn al-Haytham remarked, some ideas were rejected because certain evidence did not support those ideas. Eventually, a theory of gravity was constructed. A theory of gravity is a system, a world view about why an object that rises, eventually falls down.
A theory comprises of different laws. For example, Newton’s law (F = ma) is part of the theory of gravity. Another law that is part of it could be that ‘acceleration of an object thrown upwards and eventually coming down is because of the gravitational pull’. A law is generally expressed as a mathematical recipe also called a formula. Laws build up a theory along with conjectures and explanations. Therefore, a theory is a complete system with laws becoming its ingredients.
A theory might work in certain circumstances only. Let me give you an example of the limitations of this theory. I have here with me an object, a ball. What material is this? It’s metal. It must obey the law of gravity. If I throw this ball up, it will come down under the action of gravity at a certain speed. As it comes down, will its speed change?
PARTICIPANT: Yes.
SABIEH: But will the speed increase or decrease?
PARTICIPANT: Remains constant.
SABIEH: If I stand on this chair and jump down, nothing happens to me, but if I stand on the ceiling and fall down, I will get hurt. Why will I get hurt? That’s because my speed is constantly going up. This is why a paratrooper has to slow down and decelerate. All of this makes sense because the theory of gravity is at play. The theory always works for Sabieh jumping off a cliff or a paratrooper gliding down from the sky.
Now, I take this metal ball and I am going to drop it through a pipe [Figure (1)]. Anything special about this pipe? It’s a simple hollow pipe. Focus on this screen over here. [Screen shows the camera view focused on the instrument.] I am going to just drop this ball, nothing special is going to happen and you will see the motion of this ball too. [Ball is dropped through the pipe. Nothing unusual happened.] Let me repeat. This ball is going to come down with a really high speed, we know the acceleration is about 10 meters per second per second. The theory of gravity is correct because it is corroborated by millions of observations and is defied only by pseudo-scientists whom you don’t generally want to pay attention to.
Now let’s repeat this experiment but this time with another kind of pipe. The radius is the same [Figure (1)]. [Ball is dropped through the second kind of pipe.] The ball is coming down, but now look at its motion. [The ball is seen to fall down with an extremely slow speed, apparently defying gravity.] The theory of gravity is applicable; you can’t say it is incorrect. But it has certain limitations, called the ‘scope’ of the theory.
 |
 |
| Figure 1: About gravity and apparently circumventing it. | |
Prof. Guessoum talked about relativity. Newton is one of the greatest genius and for 200 years he stood unopposed but Newton’s laws do not hold sway close to highly massive objects such as stars and black holes. The slowing of the ball is unrelated to relativity but is due to another theory, another body of knowledge that emerged between Newton and Einstein. Did I hear the word magnet somewhere? Can the biologists sitting here raise hands? Can you tell me why did this metal ball slow down as it descended the second pipe?
PARTICIPANT: There is a magnet.
SABIEH: Where is the magnet?
PARTICIPANT: Inside the pipe? Or is a ball a magnet?
SABIEH: So, you said the ball is a magnet. Or is the pipe a magnet? Touch it, is it metal?
SABIEH: Now you are making conjectures, hypothesis, and forming opinions. Why is this ball slowing down? Is it being attracted by the metallic pipe? Or being repelled? [I bring the ball close to the metallic pipe. There is no attraction apparently].
PARTICIPANT: Is the height of both pipes the same? Or maybe the diameters are different?
SABIEH: Well, well! This is an aluminum pipe, and the ball is a magnet, and there is no attraction between the two. There is another theory that comes to our rescue explaining this strange phenomenon. That theory has been developed by an illustrious line of people, starting from Volta to Gilbert to Eddy, Faraday, and Maxwell. It is called the theory of electromagnetism.
When the object falls through the pipe, it is radically slowed down because as it falls down, there are currents produced inside the pipe which makes the region an electromagnet and it opposes the descent of the ball—the process apparently defying gravity. These small currents are called eddy currents. So, here we have a new theory relevant to this new observation. You can’t claim that the theory of gravity is incorrect but only that it is limited in scope. When there are electric and magnetic currents involved, you have to look at some other theory. That other theory can also have limited scope but fill in certain gaps in yet another theory. This is an example of going from observation, to a fact, to build up a theory, which has laws within it. The law that explains the slowing down of the descending ball is called Faraday’s law. It comes with an equation, which goes like:
\epsilon=-\frac{d\phi}{dt}
Newton’s theories are an approximate description of the happening of the universe. A theory is a big collection of models. Talking about models, gases are really important. There were scientists who were studying gases for a long time. There were three of them: Pascal, Boyle and Charles [Figure (2)] . This is an example of an experiment, which identifies variables and parameters. Here, you have a flask of fixed volume so the volume is a parameter and you change a variable which is called temperature, and you also observe and measure the pressure which is a parameter. The volume changes with temperature while the pressure is kept constant.
Let’s look at this observation. You are fetching data from some experiments. The temperature is one variable and the volume another. One of them is independent while the other is dependent. There is a causal effect here [Figure (2)].

Figure 2: Plotting variables and identifying parameters, (a) shows the data and the model while (b) uses the model to predict something not directly accessible to the experiment.
Look at these blue points, you measure the temperature and volume continuously with a computer. This is the data. On top of it, can you see the continuous blue line traversing the points? This line attempts to describe the experiment as a simplified model of a bigger reality. This line is an example of a model. The data follows and represents a model. Now how does one come up with a model? It isn’t revealed upon you, rather in order to build a model, you have to know about other experiments and models. You have to train yourself in the sciences. A four-year bachelor’s degree should help you do that. Those ideas in your mind, firing neurons, help you construct a model that describes that data. For the model that you see on the graph, you can also write a mathematical equation or formula, which is the law. In this case, the proportionality between the variable volume and temperature with the constancy of the pressure parameter is called Charles’ law (V ∝ T ).
A major utility of models is that they help predict what you cannot observe directly. For example, in my lab, ice represents the lowest limit of temperature as I cannot go below the freezing point. I do not have the means to achieve, say, 100◦C. Therefore, I use a model to predict the untestable. The volume will at some point go down to zero. The model predicts the temperature at which all gases become zero volume. This point is shown in part (b) of Figure (2). This is how the cycle of science works. You get the data, construct a model to explain the data, and utilize the model to predict the unknown.
For my second demo, I reveal another interesting observation. Can you see the three beakers here in front of you? If you look at the screen here, each one has water and similar, though, not identical eggs [Figure (3)]. But the three eggs have different degrees of flotation. One beaker is pure water while I have added just the correct concentration of salt in the other two beakers so I have adjusted the density of water. In old times, density was called specific gravity. The three eggs are in a different state.
In one case, it is completely sunk, in one it floats popping its head out of the water, and in the third, it is partially submerged. This is a fact; if you adjust the concentration of your brine solution, anywhere in the world, it will happen this way. This observation leads to conjecturing why the egg is sinking in one case, partially submerged in another and floating in yet another. In order to explain this observation, one develops a hypothesis coming up with a mathematical formulation, generally called Archimedes’ principle: “every object displaces its own weight of liquid or there is an upward force on a submerged object equal to the weight of the volume that is displaced”. This law or principle allows us to float on big heavy ships, which don’t normally sink.
A scientist is not satisfied with the quality only but is really fond of quantity. Something which is qualitative remains observational but science has now transformed mostly into a quantitative endeavor. You saw a glimpse of it with Faisal, that even a biologist now has to be adept at handling data mathematically [Faisal grins!]. How do we transform qualitative data into quantitative data? I am now going to do a quantitative verification of the flotation principle which is an upgrade to observing floating eggs.
This object is now oscillating, and the force is swirling up and down, giving data in real-time. As the mass oscillates, the force keeps changing. The further it is from equilibrium, the higher the force. This is a conjecture, and you can test it with another dedicated experiment. Extend the spring further and further, and the force increases. Eventually, it will become a law and, in this case, it is called Hooke’s law. Then you come up with a theory, in this case, the theory of oscillators or the theory of elasticity which contains laws like Hooke’s law. If I submerged the table tennis ball into water [I show that to the participants], the reading on the force sensor drops to (0.4 0.1)This is just a table tennis ball, hung with a spring, and here is an instrument or tool which is measuring its weight and mass or downward pull. This device is connected to a computer, and it is measuring the force, the downward pull. That force is (0.6 0.1) N. This value and the prescription brings me to the concept of uncertainties. On the reading displayed, the fourth decimal digit is not visible and hence you are totally uncertain about that digit. There is an equal probability that the fourth hidden digit is anything from 0 to 9. So the fourth digit is randomly distributed from 0 to 9. This is called random uncertainty. The other digits that are visible are also varying. This could also be other kinds of uncertainties due to random fluctuations because this ball is being bombarded by air molecules from all sides. This is a quantitative verification that the apparent weight of a floating object is smaller than its true weight.
My third demo regarding observation and the nature of science is from “air”. Air is a mixture of gases, but the Greeks had posited a theory of four elements namely earth, air, fire, and water. Each element had its own qualities: earth sunk, air rose, fire burnt and water extinguished fire. Furthermore, the air was considered indestructible and indivisible. In the past two millenniums, science has marched along with the conquering sword of reductionism. Reductionism means taking a big piece and chunking it up into smaller pieces. You take matter and break it up into small pieces, you get atoms. Air was considered to be just one medium, but now you can show that this air also is made up of different gases, and each constituent gas is not only physically but also chemically distinct. It took thousands of years to show this was true.
A theory that held sway for centuries was of phlogiston, which proposed that when you burnt something there exists an object inside this burning object, called phlogiston, that helps in burning, and when burned, it is released into air. Finally, Joseph Priestly who was interestingly not even a formally trained scientist, but associated with the church and is credited with inventing the unitarian thought of Christianity, worked with gases and the nature of air, ended up isolating oxygen [Figure (4)]. This resulted in showing that air is indeed destructible.
 |
 |
| Figure 4: Priestley’s observations set the stage for understanding air. | |
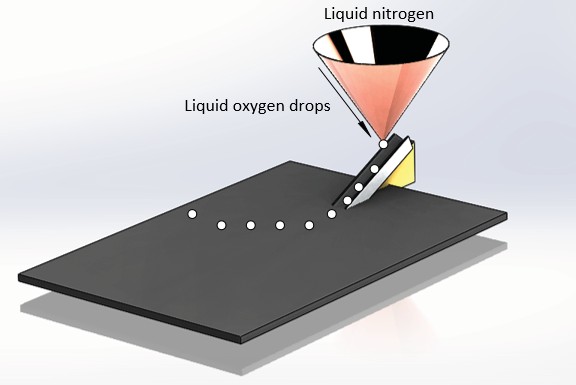
Here, I am practically going to isolate oxygen from the air, right in front of your eyes. This is a fun experiment and one of my favorites [Figure (5)]. I also love doing experiments that work at extremes. This experiment employs extremely cold temperatures to fractionally distill oxygen from the air.
What we have here is a big cone and liquid nitrogen which is at 196◦C. How many of you have seen liquid nitrogen in real? This is a flask containing liquid nitrogen. If I were to spill this over a little bit, here is what it looks like. It immediately vaporizes as soon as it comes out of the flask [Everyone looks at the liquid nitrogen with amazement!]. Now I am going to pour this liquid nitrogen into this big cone and see if I can extract something from the air. This is the top view of the surface of the liquid nitrogen at the top
of the cone. It is vaporizing because, for nitrogen, room temperature is way beyond the boiling point. Let’s focus on what we see here, look right down at the apex of the cone.
PARTICIPANT: Is it solidifying?
SABIEH: Nothing is solidifying. Look here, what is this? At this point [pointing on the video screen], can you see a dot? This is actually a magnet. I have put a magnet beneath the plexiglass sheet. Look, something is pouring down from the cone. The cone is made up of copper, an excellent thermal conductor, so the tip is becoming very cold. A liquid is collecting at the tip of the cone, dripping down the inclined plane that looks like a rail track, and finally as soon as it descends on the sheet, it is bent by the magnet. Can anyone tell me what’s going on here? What are these tiny liquid drops made up of?
PARTICIPANT: Nitrogen!
SABIEH: Why is the magnet bending the nitrogen drops? PARTICIPANT: It is ionized. It is paramagnetic.
SABIEH: No, it’s really oxygen which is indeed paramagnetic and when you put it inside a non-uniform field, it changes its direction. I bet most of you are seeing pure liquid oxygen for the first time in their lives. Boiling liquid nitrogen is at 196◦C while the cone is approximately at 190◦C. This is still below the condensation point of liquid oxygen which is 183◦C. On the surface of the cone, oxygen in the air condenses, all the oxygen drops come down the cone tip, trickle-down, coalesce and are deflected by the magnet. The scientist makes the observation that there is something magnetic about oxygen. The quantitatively minded scientist then performs a measurement of the size of the deflection, quite similar to deflecting alpha particles in the historic experiment performed by Rutherford a century ago.
Second day of lecturing starts.
SABIEH: Today’s lecture is going to be less fun than yesterday because we have some work to do. Work is less fun, isn’t it? Today, I have four or five things on my mind. Yesterday, we may haven’t said so but we talked about the interconnectedness of knowledge. This is my first premise for today. Science is related to ethics, history, and philosophy.
Today’s lecture will give you an idea of how science is also interconnected within itself. This concept is very important. I don’t know what the situation is in Algeria or Indonesia, but in Pakistan, someone who has done an M.Sc. in Zoology will be unnerved if he is presented with a mathematical equation. Similarly, a chemist would be really good at doing titrations, organic synthesis, refining, and isolating compounds or making different emulsions, but when it comes to doing quantitative analysis, she will become apologetic and will proclaim: “I can’t do this”.
The second thing I will exemplify today is how to proceed from data to model. I have distributed these graph papers just to give you an example of how this can be done. Science, over the century and millennia, has become more and more quantitative, whether we like it or not. You have equations, you have large amounts of data sometimes called ‘big data’ and finally you have algorithms and programs that sift through this data looking for order within a jumble of information. It is important to realize that you will always be presented with data and you must have certain tools on your fingertips to classify, process, and characterize the data. You can choose whatever tools that please you.
The third learning outcome is something that has somehow been overlooked in this workshop albeit unintentionally. I would like to emphasize the role of mathematical phenomena, that mathematics is at the heart of many scientific phenomena, and is rightfully also called the mother of sciences. Once upon a time, philosophy was called the mother of sciences but today maths is the common language that describes all-natural, physical, biological, and scientific occurrences. I will give you two examples and as they unfold in front of you, you will hopefully be convinced of how mathematical phenomena pop out of everyday observations.
The first example I’d like to give is from an experiment that was performed in 1824 by a Danish scientist named Hans Christian Oersted. Yesterday, I talked about the theory of electromagnetism and Newtonian theory that describes how planets moved around the sun, how the solar system is structured and how the stars themselves move. The theory of electromagnetism was a synthesis of ideas explored by scientists for over two centuries. One of the scientists who stands above many others in this line of discoverers was Oersted.
In Figure (6), you can see him performing an experiment and his peers look- ing on. This appears to be some kind of chemical lab, look at the background, maybe an apothecary. Oersted was working in the nineteenth century and this painting also reminds us of the importance of conveying experimental find- ings to one’s peers.
Oersted was already building on the works of Gilbert and Alessandro Volta, who had actually produced currents and invented the battery. So, Oersted had in front of him the means to generate currents, he knew what a battery is, whatever its primitive form we are talking about in the nineteenth century, and was able to pass a current through a piece of wire. When current flows, it can impact surrounding objects that are not even touching or making contact with the current-carrying wire. This was an astounding experiment for its times, influencing objects at a distance. It might even have appeared as magical in those times. Just imagine the excitement such an experiment would have incited in the onlookers.
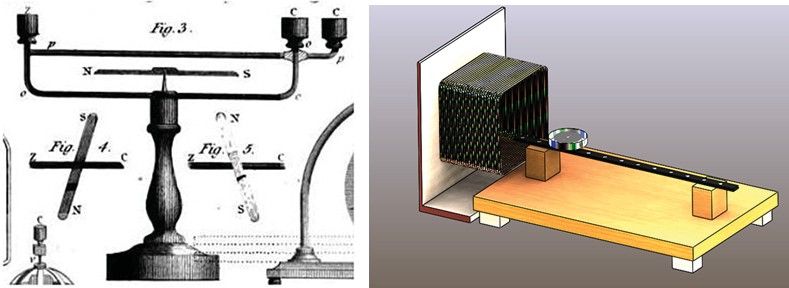
Figure 7: Oersted’s equipment shown in (a) while (b) shows a modern con- traption that I employed for the demonstration.
Figure (7)(a) shows a diagram of the equipment that Oersted was using. This picture is taken from a scientific work that gets published in a journal titled ‘The Philosophical Magazine’. Let’s imagine for a moment what is happening in Oersted’s mind. He is performing an experiment by first building an apparatus to demonstrate an idea and then making a sketch of the apparatus. The sketch is published in a journal article that describes his findings. Part (b) of the figure is a modern version and reincarnation two centuries after Oersted’s original work. Yours truly built it! There is a piece of wire, a current passes through this and there is a piece of iron called a lodestone Lodestone forms a magnetic compass. The compass has shaped how human civilization has evolved. Yesterday we saw Idrisi’s map, how in the world did he come up with his world map? Where did he get his data from? From travel and guided by pieces of lodestone like this!
[Cross talk.]
SABIEH: But I doubt he was traveling the whole known world, instead he was taking help from the travelogues and maps that were available to him, and all those travelers were making maps with the help of a compass. The compass needle is deflected in accordance with where you are in the globe. The Chinese were apt in using compasses and were expert navigators of the globe, then came the Portuguese, the French and the British. There could be a long historical episode behind any story of science that you teach to your students. This is where the interconnectedness comes to life. Here electricity and magnetism are talking to geography, world trade, and wars between empires. This is the kind of interconnectedness you can bring into your classrooms and enliven them, light them up!
Sorry, I got carried away. Let’s come back to our experiment. So this is a compass needle here. A current passes through the coil and this compass needle is deflected. This small experiment which takes just a few minutes to perform, actually has a long history behind it, of centuries and millennia. And this is how science travels in time.
We perform this experiment with a modern version of the experiment [Part (b) in Figure 7]. Let’s see for our own selves what happens to the compass needle when the current flows through a coil. Can you see the compass here? [Pointing to the apparatus on the front desk.] This apparatus is oriented in such a way that the compass is naturally pointing North as it should. This power supply is a modern form of the battery and this is a piece of the coil. The battery passes a current through the coil, with a compass placed nearby. Now, I am going to turn on the power supply. Here you go! [As I switched on the current, one could see a deflection straight away. I ramped down the current, the compass deflection goes down.] Let me switch it on again. Notice there is no mechanical contact between the compass needle and the coil, no one is touching it, but it is still rotating on its own influenced by a nearby event. If I were to change the direction of the current, aah! let me do that, this needle is going to be deflected in the opposite direction [This is precisely what happens.]
Once the observations are over, one would like to extract data from this observation. What are the variables in this experiment?
PARTICIPANT: The current.
SABIEH: Bingo! current is one variable because you can vary it. And what can you see? The angle of deflection. So, this becomes the second variable. And what are the parameters for this experiment? The size of the coil, the distance of the coil and the magnet are some fixed parameters. The number of turns and the shape and geometry of the coil are also parameters. The distance of the needle from the coil is yet another parameter. No doubt, you can always do different experiments with different parameters but for this particular instance, you have one set of fixed parameters. So, you have identified two variables: current and angle of deflection.
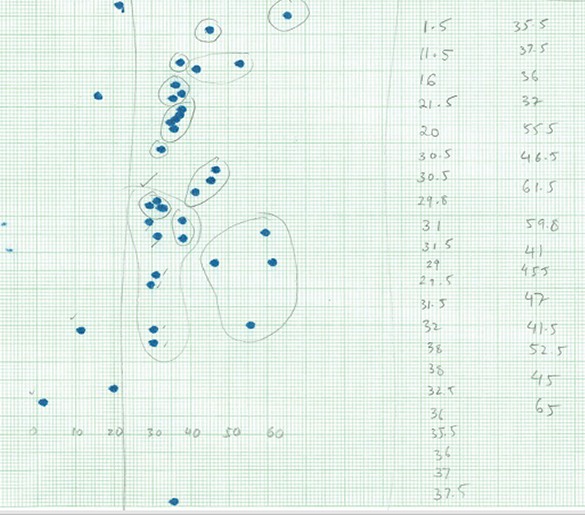
What we could do next is to have a list of the currents and a list of corresponding angles. This is shown in Table 1. I had acquired this set of data earlier and now we will work with it. I have written ‘B’ here [Table (1)] for a measure of the current. This ‘B’ is a symbol for the magnetic field but I am not going to talk much about it, only that the current is producing a field. This is a philosophical leap in science since we are proposing something that we can’t directly see. You can see the current because you can measure it with the help of a galvanometer but the field is something that you cannot directly see. It is harder to believe an unseen thing. One of the giant leaps of scientific imagination happened with electromagnetism. Ether was another hypothetical, unobservable construct that permeated the earth, but whose existence was later disproved. Likewise, the field of gravity is invisible. Hence, the human mind developed with the development of science and believed in abstractions that we can’t see. Being able to see is just a small kind of observation.
| B (Gauss) | θ (Degrees) |
| 0.097 | 20 |
| 0.121 | 24 |
| 0.146 | 26 |
| 0.194 | 30 |
| 0.218 | 32 |
| 0.243 | 38 |
| 0.291 | 40 |
| 0.316 | 42 |
| 0.364 | 48 |
| 0.437 | 50 |
| 0.485 | 52 |
| 0.534 | 58 |
| 0.631 | 60 |
| 0.704 | 64 |
| 0.801 | 68 |
| 0.922 | 70 |
| 1.165 | 72 |
| 1.432 | 78 |
Now that you have data, you would like to construct a model. That is the general sequence of events in any scientific endeavor. You make an observation, you have data, then you will like to make a model. Model building starts with making a graph. On one axis, you draw the field, and on the other, you draw the angle, and these are your points [Figure (8)]. Next is to come up with a model that fits the data.
Fitting means finding a model, a mathematical rule, or a principle that explains the data. We now attempt to construct a model. For this purpose, we invoke another branch of science called trigonometry. This is the interconnectedness of science. Physics alone is not sufficient and data alone is not sufficient. You will have to access some knowledge of mathematics, trigonometry, and its rules which were first proposed by Greeks such as Euclid and Aristarchus.
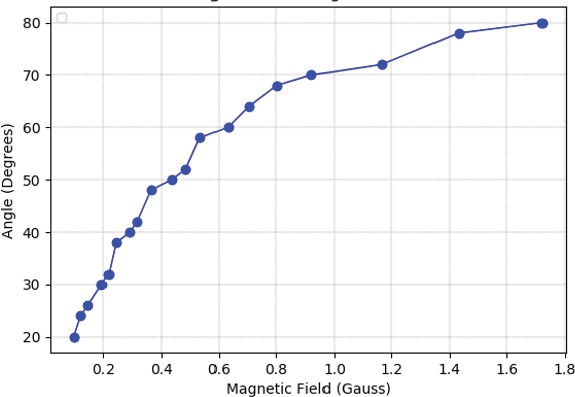
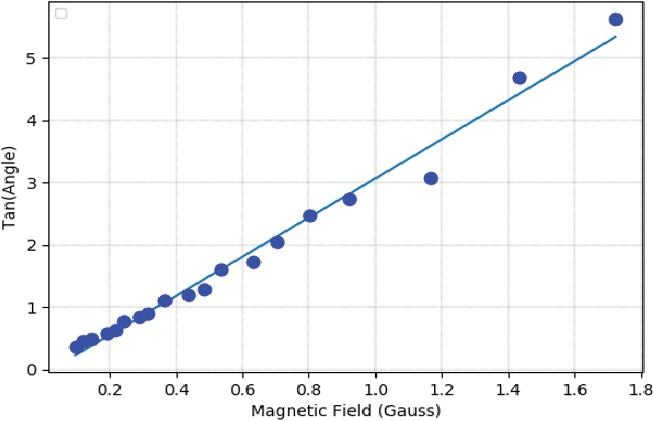
Figure 8: Graph of the angle of deflection of the compass needle versus the applied magnetic field which is a measure of the current.
A triangle is an important construct in the history of science. The history of the triangle warrants a complete episode of its own. I just suffice here to mention that in trigonometry, we define the tangent of an angle. We employ this tangent function to build the promised model.
If I were to plot the field or the current on one axis and take the tangent of the deflection angle on the other axis, we obtain the graph in Figure (9). Lo and behold, even though Figure (8) was a graph that changed its slope as it went along, Figure (9) shows that the points lie on an almost straight line. Do you remember Einstein’s quote which Nidhal mentioned yesterday? “Science should be made simple but not simpler”. What is the simplest model that you can think of? The simplest model is that Ali and I are standing here and if I go up then Ali also goes up, I go down, Ali goes down so that is the simplest model you can think of. If one thing goes up, the other goes up, two variables are working in tandem and unison. And you can’t make it any simpler. Anything simpler than that is constant, just remain where you are. But that is not interesting at all. The simplest model you can think of, therefore, is a straight line and Figure (9) indeed produces a straight line called a linear model between tan(angle) and the magnetic field.
That is the craft of model building. One can massage or manipulate (not
fudge!) the raw data, transform the variables, and create as simple a model as possible. And you can’t do this out of your whims. You have to be intelligent and you have to have some knowledge e.g. what is a magnetic field? What direction is the earth’s field pointing in? What direction is your applied field pointing in? Does the geometry have something to do with trigonometry? That is where your knowledge and training is put to good use. Then you build this linear model [Figure (9)] after which you describe and explain the data and predict all kinds of fancy and unusual things.
Once, you have a model, there is an entire world in front of you and you can start explaining, why do you have this particular model? What are its limitations? If I keep on increasing the magnetic field, what is going to happen to the angle? Can the angle even go beyond 90◦? These are the questions that you would like to ask. You would like to put extreme tests on your experiment. This is a glimpse into the mind of a scientist.
Whatever kind of scientist you are, a Nobel Laureate, or just a beginner, a novice like myself, these are the kinds of notions that must be going on in your mind. And it is important to understand, to live the scientist if you want to be a teacher of science. How do you teach this to students? You teach by example. You don’t tell them everything and they don’t memorize this journey from data to model, you rather give them examples. And then you tell them how things work, they work through it and then you point out that this is ‘data’, this is ‘the model’, this is a ‘conjecture’ and this is a ‘graph’ that you have to draw [Figure (10)].
In the history of science, one encounters tools and instruments, and in fact these tools and instruments are really important. There are some areas of science and technology where the tools came before the theory. Can you think of such a branch of science or technology?
Look at the industrial revolution and probably Dr. Abubakr is going to talk a little bit about the steam engine. When the engine was invented by James Watt, there was no theory of thermodynamics available neither was there any kinetic theory of gases. But the tool and instrument came into existence. Similarly, in the 1870’s, wireless signals were transmitted and received but there was no theory of communication yet available, the theory of electromagnetism had just been synthesized but Henry Hertz had demonstrated the technology. There are examples in which the tool came before the idea. Tools and ideas, in fact, both go together. Sometimes ideas win the race and they lead to the discovery of tools. The structure of DNA for example came after the tool of X-rays was known.
Tools are extremely important and we need to understand what roles tools, gadgets, and instruments have to play in the history of science. These are all the kinds of ideas you would like to communicate to your students. Look at the big picture, for God’s sake [Sabieh gets emotional!]. Don’t take the trees for the forest. Tell the students what the tree is, what the bark looks like, how the stem is, how the plant looks like. But let your students know the forest as well. That is the interconnectedness, the holistic idea we would like to relegate onward to the students.
When there is data, choosing your variables is the first step. Choose your parameters and in most cases, then you would like to classify your variables as independent or dependent. You would then like to present your data in an appropriate manner. You would like to make a graph, a sketch, an illustration, a table, an animation, or a video. Present your data in a way that is easy to understand, and then you build a model. This last point, I would really like to highlight, the scientific enterprise does not work in a vacuum, it is not just you and the classroom, it is not a one to one relationship between you and the teacher, it is actually a big ecosystem out there. There are journals, there are periodicals, meetings, networks, video logs, blogs, and who can forget the internet. These are a medium for communicating scientific results. All of this has to be factored in if you want to train the scientists of tomorrow.
The next point of discussion is about the concept of ‘uncertainty’. Can we bring the Galton board, please? Now I have intentionally put this ayah from the Quran [Recites Ayah from the slide.]

In fact, I have introduced this ayah just for the reason that there is another way to look at nature between the scientific work you do and the scripture that you read, for Muslims, the Quran. That is of inspiration. In the course of human civilization, especially when Muslim scientists were at their heyday, there was a lot of inspiration from the Quran. But that does not mean to say that the Quran is a book of science. The Quran doesn’t teach algebra or metrology, how do we measure and what are its rules, it just gives a general principle of honesty and metrological integrity. Your weights should be proper, that is a general economical, ethical principle that is laid down by the Quran. And then it is the scientist who actually goes into the field, and tries to come up with a metrological system. Measurement as you all know is extremely important as depicted by these folios from the Egyptians, pharaonic times [Figure (11)].
 |
 |
| Figure 11: Role of measurements has been important from Pharaonic times. | |
I would now like to present to you an example of a curve, which is really important in the theory of measurements and uncertainty. Prof. Nidhal used the terms 1σ, 2σ, and 3σ. I would like to give you a practical demonstration of what are these σ’s. For that purpose, I have in front of you an invention attributed to a European scientist Galton. He made this board as a demonstration to teach about probability, which is central to the concept of science. This is an idea we must understand thoroughly.
A scientist is not known for his idealism but he is known for his appreciation of uncertainty. That is how I define a scientist. The layman thinks that the scientist knows everything accurately, that we are perfectionists, accurate, and extremely precise. If my students perform an experiment in the Physlab and I ask them to come up with an experiment to measure the value of acceleration due to gravity, someone comes up with 9.7 m/s2, someone comes up with 10 m/s2, but then all of a sudden a group of students euphorically run up to me and exclaim “Oh Sir!” we have measured g at 9.8 m/s2. I hasten to dampen their euphoria and ask them “What is your uncertainty?”.
Now, I am going to give you a demonstration of this board right here. You can see this board has pegs in it, and these are marbles, right? Can I have a volunteer? Can you also see this? [Lifts board.] I am going to turn it around so you don’t see how this is progressing and only see the final result. [To the participant:] “just put these marbles into the board one by one and start from the middle. Any questions in the meantime?”Their result may be accurate but they have to quantify their uncertainty. So, they should say our value of g is (9.8 0.2) m/s2 with a coverage interval confidence of 95%, something of that kind which completely quantifies their statement. Similarly, suppose you measure the mass of this block, you weigh it, and then you wait after a second, re-weigh on the same scale, you may get a slightly different reading. I run this around the whole class, everyone may get a slightly different reading. There is some distribution, some curve that you will always fetch. This is quite natural, is nothing wrong with it, don’t be apologetic about it. This is just how nature works.
PARTICIPANT: Is it possible to do all this in a classroom?
SABIEH: Of course! Any reason why can’t you do it in the classroom?
PARTICIPANT: Lack of resources. . .
SABIEH: You have to teach the children, right? Your generosity and commitment should be bigger than the lament of the lack of resources. We are not saying you have to reproduce this exactly, but at least try. You have to pour knowledge into minds so your ken should be bigger. You have to intelligently come up with new demos, new contraptions, new tools, and new gadgets. It’s not always about money, it’s about time and the fire that burns inside you.
PARTICIPANT: Our syllabus is rapidly changing. The things we studied in college, we are now teaching in matriculation (school) and things we teach in matriculation are now being taught in grade eighth.
SABIEH: The example I gave you of eggs yesterday, can you not do it with your class?
PARTICIPANT: I teach grades ninth and tenth and we teach magnetic lines and Faraday’s law, but we can’t demonstrate its implementation. But your lecture has helped us understand how we can explain it to the students.
SABIEH: Look, let me give you my general thought about this. You have to think big. Your benchmark is not your curriculum. Your benchmark is the world at large. Your curriculum is your constraint but should never become the benchmark. Idealize for bigger things and your benchmark should be the bigger thing out there. That is why we are here, so, take these examples. No one is asking you to replicate them. Replicate the ideas. Build your own models. If you are a teacher you must build your own instruments, apparatus, and demonstrations. That is the goal of this workshop.
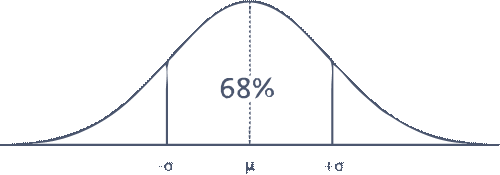
Alright, coming back to the Galton board, let’s turn it around. It is not the way I intended, but this is what the distribution looks like. It’s slightly skewed but that’s alright. You would see that there is a maximum somewhere. I have separated out the bottom pieces into bins. If the beads were more numerous, there is a bin that has the maximum likelihood of receiving these. But, not all the marbles get into that bin, there is a whole wide distribution. Ideally, if this was a large Galton board, and if there was no bias that I introduced while dropping these balls, I would get a curve that looks like a Bell curve [Figure (12)].
If there was no uncertainty, then all of the marbles would fall into the same slit. Would such a thing ever happen? As far as I can tell, “no”. By its very nature, natural phenomena follow such as distribution. There is always
a maximum likelihood position. Most natural processes follow a distribution of this kind, called a Bell or Gaussian distribution. If I go to the left or to the right from the most likely bin by one sigma (σ) and if I counted all the marbles in this region, they will be approximately 68% of all the marbles. This unit of length is called 1σ, which means that 68% of the marbles are likely to fall in between +1σ and 1σ of the average. Similarly, 95% of them will fall between +2σ and 2σ. That is what the sigma value means. So, if you do an experiment, and you quote the value of sigma, how large your sigma is, you can then be confident that 68% of your outcomes are going to lie between +1σ and 1σ of the
a non-zero sigma.
Science inherently values uncertainty, and here I am not talking about quantum mechanics, which just completely topples over our concept of uncertainty, I am talking about normal natural phenomena.
Now another demonstration that you could do for your class is to obtain an inclined plane, and on the bottom, place a piece of carbon paper. Then, it could take a ball, metal, or something hard that can leave a mark on the carbon paper. Drop it from the top of the inclined plane so it just falls on to the carbon paper. Repeat this experiment a large number of times, exactly from the same position. Let me do this 10 times right in front of you. Then let’s do it five more times. Okay. What do you predict to see on the carbon paper below? A splatter of points?
PARTICIPANT: Variation?
SABIEH: There will be some variation. No doubt about it. This is what you will observe. [I show the carbon paper [Figure (13)] with the ball markings, all in different positions.] This is a raw observation. I could also go to extra lengths of having the same initial conditions for each experiment. I could for example build a track on this inclined plane, so that the ball always starts on the same place on the inclined plane. If I have the time and the money, I could also remove all the air from this room, making it a perfect vacuum.
I need to figure out how to breathe then! but let’s forget that. I could also remove myself, a human from the picture, and have a robot, Sabieh-bot performs this experiment. There is still going to be clutter, the spread can go up and down. But there has to be a spread, always! No escape! When you look at this variation, you could do a mathematical analysis. Your students can do this, grade six students can do this. Nothing fancy or expensive here. Carbon paper and a human mind. That’s it! They can point where the ball hits on the paper and position the outcomes on a histogram. The histogram will resemble a Bell’s curve.
In fact, not only grade sixth, seventh or eighth students love doing this, undergraduates in LUMS also love doing it. I think it teaches them something useful which they haven’t seen anything of this kind before. Science by its nature has an element of humility built into it due to this very uncertainty. Let’s begin to appreciate this.
Another pertinent point before I forget: Prof. Nidhal mentioned the age of the universe, 13.787 billion years, now he was honest because he also mentioned 0.020 billion years at the 1σ value. He was honest in two ways. First, he is quoting an uncertainty. Fifty years ago the age of the universe was much longer, it isn’t that the age has reduced, it is only that our estimates have become more accurate. Second, notice the trailing zero after the 2 in the figure 0.020. The number is logically the same as 0.02 but scientifically the ‘0’ at the end has a meaning. It is significant and that is why he quoted it. A scientist has to be honest to the core and must accurately present his uncertainties.
Finally, we are coming to closure to my contribution to this workshop. In the last part of my presentation, I would like to highlight the role of mathematics because this is something that has been slightly ignored, even though unintentionally. This is an object that we made in our lab [Figure (14)]. This problem actually goes back to the time of Greeks, but the first scientist who studied this problem was really Fermat and the problem was then taken up by Bernoulli and later by Galileo. This is a historic experiment. You can teach it to sixth to eighth graders and to university students too, and you will have different messages for them. I am going to highlight the role of maths in this particular demonstration.
Folks, do you know what the speed of an object is? How will you find out the speed of something? If you are going in a car and want to find the speed, how will you measure the speed?
PARTICIPANT: Measure distance and time.
SABIEH: One variable is distance and one is time, your distance is 1 Km and time is 1 hour, what will be the speed? Any biologist who would care with an answer?
PARTICIPANT: One meter per second.
SABIEH: No! 1 Km per hour. So the speed is how far you travel and how long does it take. Then you take the distance you have traveled and divide it by time. If you have the speed and distance, you can also find out how long does it take. If I want to go to Islamabad, 350 Km away, and I am moving at a speed of 100 Km/h, I can find the time. It is 3.5 hours.
OK, so far, so good. Here, let’s move to our experiment in front of you [Figure (14)]. I have two paths. Which path is longer?
PARTICIPANT: The curved one.
SABIEH: Okay, just observe, don’t memorize anything. Is the curved one longer? Which one has more material in it? More volume?
PARTICIPANT: The curved one.
SABIEH: Yes! Since this has more mass in it, it is longer. If I released two balls at the same time from the end part of both of these paths, which ball will reach first? This seems like a pretty common sensical question.
PARTICIPANT: The straight one.
SABIEH: Straight one of course, the smaller the path, the quicker it will come down. Right, so let’s see, I am going to release both these balls coincidentally [Both balls are released.] Which came down first?
PARTICIPANT: The straight one.
SABIEH: Let’s repeat. Observe carefully and then I will later show a video for this. [Both balls are released again.]
PARTICIPANT: [Changing her mind] The curved one.
SABIEH: Your observation is correct. Who else corroborates the observation that the ball on the curved one came down earlier? [Most participants raise their hands].
It is not a miracle happening here. I am not a wali and cannot change the course of nature! But your raw observation is that the ball came down quicker on the curved path, even though the path is longer. Good grief! How is this possible? Now, how do you answer this question?
First of all, you have already mentioned that gravity has a role to play. The acceleration due to gravity, the force with which the earth is pulling down the ball, is different for each of these paths. Here [pointing to the straight path] it is constant and does not vary along the path, though it is not equal to g, and here [pointing to the curved path], it is changing all along the path. Where the curve is steeper, the velocity is smaller, which also means that the acceleration is larger. Here, where the curve becomes flatter, the acceleration is smaller but the velocity could be the highest. All of this looks terribly complicated. How do we solve examples of this kind? You need recourse to mathematics. It is slightly difficult mathematics but the difficult math really simplifies the problem. If I were to be a better student, I would have tried to do this problem for the first time when I initially learned about integrals. A beginner university student may be able to answer this but at least you as teachers should try to invoke the mathematical sense of your students with examples of this kind.
I will play the video for this now, and you can observe that for the two objects released at the same time, the one on the curved path comes down quicker. In fact, a whole branch of mathematics was invented to solve problems of this kind. It is called the ‘calculus of variations’. Can I have a piece of wire? A USB cable or something? [I hold a wire from one end and another person holds from another, horizontally.] This piece of wire is taut and horizontal because both of us are holding it and our hands are at the same height, with some uncertainty of course. Now, I move one of the ends to a higher level, what is the shape of this? A curve, of some weird kind. I changed the height without changing the length. This is an observation, a real-life observation, but you need mathematics to describe it and model the shape this curve assumes. This was a problem solved first by the Greeks, and the greatest Greek mathematical minds were involved in finding the shape of this wire. Maths is everywhere in this, it is an inescapable body of knowledge that permeates discussions of this nature.
Finally, while Azeem physically sets up this structure, look at this arrange-
ment here in Figure (15). It is an innocent and innocuous arrangement of blocks just stacked on top of one another. Any student can do this. My intent is to arrange them in such a way, that my overhang, that is how much do I extend from the base of the bottom block, is the maximum. You can have your students spend an entire day in maximizing the overhang. The beautiful problem, much like Ludo or snakes and ladder. If I go a little over, it might tip over but that is fine. If you observe this pattern here, the top block is overhanging by a larger degree. The bottom one is overhanging by some degree which is smaller than the top, and the pattern continues till the very bottom.
You can also quantitatively measure the overhang using a piece of chalk and marking the blocks. The overhangs become similar and smaller as you reach the base of the structure. Something simple and easy, but an astounding mathematical pattern emerges from them. And I say this again, science is beautiful. I can say it loud and clear “Science is mesmerizing”. In fact, most people do science because they are pulled by its aesthetic appeal. The sequence of measurements begins to look like this:
\frac{1}{2} \left(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\dots \right).
This is actually a nice rendition of a mathematical phenomenon. Dear all, thanks, it was a real pleasure talking to you all.
References
1Ibn al-Haytham’s introduction to Doubts concerning Ptolemy, translated by Jamil Ragep, McGill University
2Mathematical Aspects of Physics: An Introduction, Francis Bitter, (Anchor Books, New York 1963)