Class Timings and Venue: 5 pm to 6:15 pm, Monday/Wednesday in 10-201.
Instructor: Muhammad Sabieh Anwar
Office Hours: 3 pm to 5 pm, Monday/Wednesday.
Class TA: M. Abdullah Ijaz
Office Hours: 4 pm to 5 pm, Monday/Wednesday in 9-109.
Course Code: CS 5112 / EE 539 / PHY 612
Link to the video playlist: Here
Fundamentals of Quantum Information Science:
- The qubit: quantum states, quantum degrees of freedom, photons, electrons
- Quantum interferometry: Bloch sphere, Mach-Zehnder interferometry, measurement and complementarity, unique features of quantum states
- Quantum Transformation: Dynamics, invariance, Pauli matrices, unitary gates and their action on the Bloch sphere
- Quantum Dynamics: Spin 1/2 particle, Schrodinger equation, Hamiltonian and time evolution on the Bloch sphere
- Multi-Qubit Systems: Entanglement, outer product, tensor product, controlled NOT gate and separability
Quantum Algorithms:
- Quantum Teleportation: No-cloning theorem, teleportation scheme and quantum circuit
- Deutsch-Jozsa Algorithm: Quantum Oracles, superposition and the advantage of relative phase
- Grover Search Algorithm: Grover Oracle, diffuser, geometric progression and gate implementation
- Quantum Fourier Transformation Algorithm: Discrete Fourier transform, binary and decimal ket notation and discrete Kronecker delta function
- Quantum Fourier Transformation Circuit: Quantum Fourier on arbitrary n qubit state, controlled rotation and SWAP gate
- Quantum Phase Estimation: QPE algorithm, corresponding circuit and MATLAB simulation of inverse quantum Fourier transform
- Shor’s Factoring Algorithm I: Period finding, prime factorization, Kitaev’s implementation and quantum factoring algorithm
- Shor’s Factoring Algorithm II: Kitaev and quantum phase estimation implementation and corresponding circuit
Quantum Communication:
- Density Matrices I: Density matrices, projection operators, pure and mixed states and purity of a quantum state
- Density Matrices II: Block vector notation, tomography, dynamics, the Liouville Von Neumann equation and bipartite states
- Density Matrices III: Separability, partial trace and partial transpose
- Classical Information: Bayes theorem, concave functions and Shannon’s entropy
- Quantum Information: Quantum Shannon entropy, mutual and conditional quantum entropy
- Classical Encryption I: One pad scheme, Euler’s function, congruences and primitive roots
- Classical Encryption II: Diffie-Hellman and RSA encryption
- Quantum Key Distribution: Photonic QKD and BB84 protocol
- Quantum Information II: Bell’s Inequality and Nonlocality
Quantum Technologies:
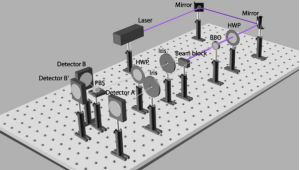
- Single Photon: Laboratory Setup, non-locality tests, tomography and quantum interference
Assignments:
- Assignment 1 | Solution Manual 1
- Assignment 2 | Solution Manual 2
- Assignment 3 | Solution Manual 3
- Assignment 4 | Solution Manual 4
- Assignment 5 | Solution Manual 5
Exams:
Project: Instructions